Solved

Use Euler's Method with Step Size to Approximate

Question 11

Essay

Use Euler's method with step size 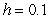Use Euler's method with step size to approximate where is the solution to the initial value problem . to approximate Use Euler's method with step size to approximate where is the solution to the initial value problem . where Use Euler's method with step size to approximate where is the solution to the initial value problem . is the solution to the initial value problem Use Euler's method with step size to approximate where 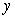is the solution to the initial value problem . .

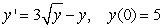Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: A rat population for a certain field

Q7: A tank in the shape of a

Q8: Use Euler's method with step size <img

Q9: Solve the initial value problems.<br>A) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q10: Use Euler's method with <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Use

Q12: Find all the curves <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find

Q13: Consider the initial value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q14: A conical tank filled with water has

Q15: A deer population for a certain area

Q16: Solve the initial value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"