Essay
Let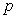 
be a population of insects that is modeled by the logistic equation: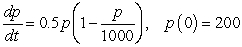 
A) Determine the equilibrium solutions and their stabilities.
B) What is the long term behavior of the population?
C) Find the value of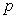 
at the inflection point and explain its meaning referring to the population growth.
D) Solve the logistic equation and verify your answer to B.
Correct Answer:
Verified
A) 
(unstable), (stable)
B) T...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
(unstable), (stable)B) T...
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q49: Bees in a certain region are born
Q50: Solve the differential equation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Solve
Q51: Solve the following equations.<br>A) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Solve
Q52: Twenty panda bears were brought to a
Q53: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let be
Q55: Use Euler's method with <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Use
Q56: Find all the curves <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find
Q57: The graph of an increasing function <img
Q58: The curves orthogonal to the solutions of
Q59: The differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The differential