Solved

A Plate Occupying the Region Bounded by the Functions

Question 62

Short Answer

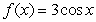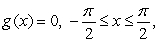A plate occupying the region bounded by the functions A plate occupying the region bounded by the functions and is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate? and A plate occupying the region bounded by the functions and is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate? is submerged vertically so that the top of the plate is under 5 m of water. What is the fluid force on the side of the plate?

Correct Answer:

verifed

Verified

approximat...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q57: In the following figure, the centroid of

Q58: An infinite plate shown in the figure

Q59: An infinite plate shown in the figure

Q60: Calculate the Taylor polynomial <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Calculate

Q61: Which of the following are Maclaurin polynomials

Q63: Four particles with masses of 4, 5,

Q64: A water tank is a rectangular tank

Q65: The quotient <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The quotient

Q66: Calculate the Maclaurin polynomial <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Calculate

Q67: The plate shown in the figure, determined