Solved

Let Be an Invertible Function Such That and

Question 97

Multiple Choice

Let 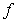Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. be an invertible function such that Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. and Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. . Let Let 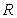be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. 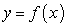be the region enclosed by the graphs of Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. 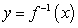and Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. 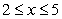over the interval Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. . 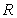The centroid of Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. lies on


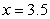A) the line Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. .
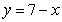B) the line Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. .
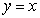C) the line Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. .
D) It depends on the function Let be an invertible function such that and . Let be the region enclosed by the graphs of and over the interval . The centroid of lies on A) the line . B) the line . C) the line . D) It depends on the function . E) none of the above. .
E) none of the above.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q90: Find the center of mass of the

Q91: Find the center of mass of the

Q92: The quotient <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The quotient

Q93: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let be

Q94: Find the centroid of the region lying

Q95: The plate determined by the region between

Q96: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="If is

Q98: The centroid of the region enclosed by

Q99: Find the centroid of the shaded region

Q100: Calculate the Taylor polynomial <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Calculate