Solved

Let

Question 8

Essay

Let 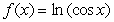Let . A) Write the Maclaurin polynomial for . B) Use Taylor's Theorem for to write an integration formula for . .
A) Write the Maclaurin polynomial Let . A) Write the Maclaurin polynomial for . B) Use Taylor's Theorem for to write an integration formula for . for Let . A) Write the Maclaurin polynomial for . B) Use Taylor's Theorem for to write an integration formula for . .
B) Use Taylor's Theorem for Let . A) Write the Maclaurin polynomial for . B) Use Taylor's Theorem for to write an integration formula for . to write an integration formula for Let . A) Write the Maclaurin polynomial for 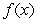. B) Use Taylor's Theorem for 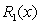to write an integration formula for . .

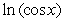Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q3: Compute the arc length of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q4: Find the centroid of the shaded region

Q5: A thin plate shown in the figure

Q6: Compute the surface area of revolution of

Q7: Find the area of the surface obtained

Q9: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute for

Q10: Find the centroid of the shaded region

Q11: Calculate the Taylor polynomial <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Calculate

Q12: An infinite plate occupying the region bounded

Q13: Compute the surface area of revolution of