Essay
The height of sixth grade students in a class is a random variable 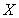 with mean
with mean 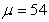 in. Assume the height of the students is normally distributed with standard deviation
in. Assume the height of the students is normally distributed with standard deviation 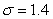 in. Let
in. Let 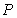 be the probability that a student will be at most
be the probability that a student will be at most  in. tall. Express
in. tall. Express 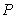 as an integral of an appropriate density function, and compute its value numerically.
as an integral of an appropriate density function, and compute its value numerically.
Correct Answer:

Verified
Correct Answer:
Verified
Q35: A cereal-packaging company fills boxes on average
Q36: Compute the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute the
Q37: To show that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="To show
Q38: The height of sixth grade students in
Q39: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate the
Q41: Evaluate the integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate the
Q42: Evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Evaluate ."
Q43: Use the error bound to find a
Q44: To show that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="To show
Q45: Calculate the following integral in terms of