Solved

The Base of a Solid Is the Region Bounded by the

Question 9

Essay

The base of a solid is the region bounded by the The base of a solid is the region bounded by the -axis and the semi-ellipse Each cross section perpendicular to the base and parallel to the -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. -axis and the semi-ellipse The base of a solid is the region bounded by the -axis and the semi-ellipse Each cross section perpendicular to the base and parallel to the -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. Each cross section perpendicular to the base and parallel to the The base of a solid is the region bounded by the 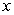-axis and the semi-ellipse 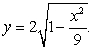Each cross section perpendicular to the base and parallel to the -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. The base of a solid is the region bounded by the -axis and the semi-ellipse Each cross section perpendicular to the base and parallel to the -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid. The base of a solid is the region bounded by the -axis and the semi-ellipse Each cross section perpendicular to the base and parallel to the -axis is an isosceles triangle whose height is twice its base. Find the volume of this solid.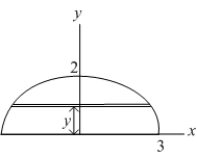

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: Find the value of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find

Q5: Find the volume generated by revolving the

Q6: Find the area of the region shown

Q7: Find a value <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find a

Q8: A chain weighing 25 pounds per foot

Q10: Find the volume generated by revolving an

Q11: What is the average volume of a

Q12: Use the Shell Method to find the

Q13: The vertical tank shown in the figure

Q14: Find the area of the region bounded