Solved

Which of the Following Functions Has a Local Maximum at a Point

Question 73

Essay

Which of the following functions has a local maximum at a point in the interval Which of the following functions has a local maximum at a point in the interval : A) B) C) D) :
A) Which of the following functions has a local maximum at a point in the interval : A) B) C) D)
B) Which of the following functions has a local maximum at a point in the interval : A) B) C) D)
C) Which of the following functions has a local maximum at a point in the interval : A) B) C) D)
D) Which of the following functions has a local maximum at a point in the interval 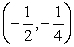: A) 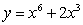B) 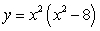C) 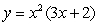D)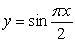

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q67: Show that the equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Show

Q68: Use Newton's Method to approximate the only

Q69: Find the intervals on which the function

Q70: The minimum and maximum of which of

Q71: Show that the equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Show

Q72: Find all the critical points of the

Q74: Estimate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Estimate using

Q75: Find the intervals on which the function

Q76: The following is the graph of <img

Q77: Estimate the roots of the equation <img