Solved

Suppose That Is Differentiable for , Is

Question 30

Multiple Choice

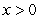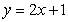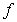Suppose that Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. is differentiable for Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. 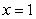, Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. 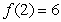is the tangent line to the graph of Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. 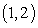at Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. 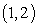and Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. . The following can be concluded:


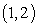A) Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. is concave up on Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. .
B) Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. is not concave down on Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. .
C) Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. is concave down on Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. .
D) Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. is not concave up on Suppose that is differentiable for , is the tangent line to the graph of at and . The following can be concluded: A) is concave up on . B) is not concave down on . C) is concave down on . D) is not concave up on . E) None of the above. .
E) None of the above.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q25: The function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The function

Q26: The following function has a local minimum

Q27: Match the functions with their graphs<br>(a) <img

Q28: The function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The function

Q29: Find the dimensions and the area of

Q31: Sketch the graph of the function <img

Q32: Estimate the length of the hypotenuse in

Q33: The increase/decrease intervals of the function <img

Q34: Find the sides of the isosceles triangle

Q35: Apply Newton's Method to <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Apply