Solved

Show That the Equation Has a Solution in the Interval

Question 13

Short Answer

Show that the equation Show that the equation has a solution in the interval and use Newton's Method to approximate it to within an error of at most . has a solution in the interval Show that the equation has a solution in the interval and use Newton's Method to approximate it to within an error of at most . and use Newton's Method to approximate it to within an error of at most Show that the equation has a solution in the interval 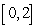and use Newton's Method to approximate it to within an error of at most . .

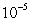Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q8: The following table describes the signs of

Q9: Given the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Given the

Q10: Find the dimensions and the perimeter of

Q11: A right circular cylinder is to be

Q12: Estimate the roots of the equation <img

Q14: A ball produced on an assembly line

Q15: Find the maximum value <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find

Q16: A producer can sell <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="A

Q17: A cylinder of radius <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="A

Q18: True or False: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="True