Solved

Let , Be Functions and Let

Question 32

Multiple Choice

Let Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. , Let 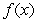, 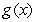be functions and let 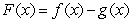. Consider the following statement: If 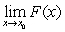and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. 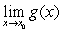be functions and let Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. . Consider the following statement:
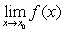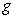If Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. and Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. 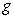exist then also Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. exists.
To prove this statement we should use:


A) The statement is not true.
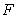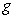B) The Product Rule applied to Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. and Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. .
C) The Quotient Rule applied to Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. and Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. .
D) The Sum Rule applied to Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. and Let , be functions and let . Consider the following statement: If and exist then also exists. To prove this statement we should use: A) The statement is not true. B) The Product Rule applied to and . C) The Quotient Rule applied to and . D) The Sum Rule applied to and . E) None of the above. .
E) None of the above.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q27: Evaluate the limits using the Limit Laws:<br>A)

Q28: Find the constants <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find the

Q29: Evaluate the limits using the Limit Laws:<br>A)

Q30: True/False:<br>If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="True/False: If

Q31: Which of the following functions has a

Q33: Determine whether the function is left or

Q34: The flight-time of a shell shot at

Q35: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="If and

Q36: To show that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="To show

Q37: Evaluate the limits using the Limit Laws:<br>A)