Solved

If and Then Does Not Converge to a Finite

Question 76

Multiple Choice

If 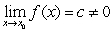If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. and If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 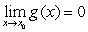then If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 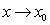does not converge to a finite limit as If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. .
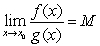For proving, we assume that If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. exists and is finite. Then
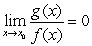By the Quotient Rule If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 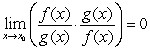and by the Product Rule If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. .
Which of the statements below completes the proof?


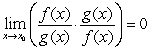A) From If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. , it follows that 1=0, which is a contradiction.
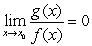B) From If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 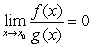, we can conclude that If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. , which contradicts our assumption.
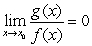C) From If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 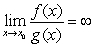, we can conclude that If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. , which contradicts our assumption.
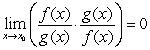D) From If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 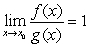, we can conclude that If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. , which contradicts our assumption.
E) A and C are correct.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q71: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let denote

Q72: Evaluate the limits using the Squeeze Theorem,

Q73: Compute the following limits:<br>A) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute

Q74: Determine the one-sided limits at <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg"

Q75: The volume of a cone of radius

Q77: Draw the graph of a function <img

Q78: Find the points of discontinuity and state

Q79: The following functions are examples of the

Q80: At each point of discontinuity state whether

Q81: Assume <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Assume is