Solved

The Following Function Is a Counterexample for the Converse of the Intermediate

Question 67

Multiple Choice

The following function is a counterexample for the converse of the Intermediate Value Theorem, which states:
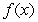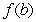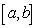If The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on assumes all the values between The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on and 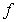The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on in the interval 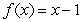The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on , then 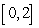The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on is continuous on 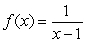The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on :


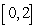
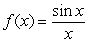A) The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on on The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on
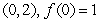
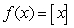B) The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on on The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on
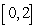
C) The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on on The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on
D) The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on on The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on
E) The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on on The following function is a counterexample for the converse of the Intermediate Value Theorem, which states: If assumes all the values between and in the interval , then is continuous on : A) on B) on C) on D) on E) on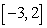

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q62: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find such

Q63: Compute the following limits:<br>A) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Compute

Q64: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let be

Q65: Which of the following statements show that

Q66: At each point of discontinuity state whether

Q68: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find ."

Q69: Calculate the limits<br>A) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Calculate the

Q70: Determine the points at which the following

Q71: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let denote

Q72: Evaluate the limits using the Squeeze Theorem,