Solved

Suppose There Exists , So That for Any

Question 25

Multiple Choice

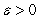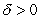Suppose there exists Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. , so that for any Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. we can find Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. 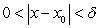satisfying Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. 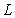and Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. . We may conclude that:


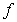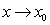A) Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. is the limit of Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. 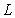as Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. .
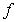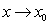B) Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. is not the limit of Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. 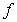as Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. .
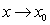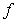C) The limit of Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. as Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. does not exist.
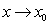D) The limit of Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. as Suppose there exists , so that for any we can find satisfying and . We may conclude that: A) is the limit of as . B) is not the limit of as . C) The limit of as does not exist. D) The limit of as exists but is not equal to L. E) none of the above. exists but is not equal to L.
E) none of the above.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: Determine <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Determine and

Q21: Find all values of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find

Q22: Use the Squeeze Theorem to evaluate the

Q23: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let .

Q24: The Intermediate Value Theorem guarantees that the

Q26: Evaluate the limits in terms of the

Q27: Evaluate the limits using the Limit Laws:<br>A)

Q28: Find the constants <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Find the

Q29: Evaluate the limits using the Limit Laws:<br>A)

Q30: True/False:<br>If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="True/False: If