Multiple Choice
When a spring is stretched and then released, it oscillates according to two laws of physics: Hooke's Law and Netwon's Second Law. These two laws combine to form the following differential equation in the case of free, undamped oscillation: 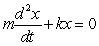 where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point) , t is time, and k is a constant associated with the strength of the spring. Consider a spring with
where m is the mass of an object attached to the spring, x is the distance the spring is stretched beyond its standard length with the object attached (its equilibrium point) , t is time, and k is a constant associated with the strength of the spring. Consider a spring with 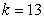 from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that
from which is hung a 40-pound weight. The spring with the weight attached stretches to its equilibrium point. The spring is then pulled 7 feet farther than its equilibrium and released. Find a particular solution for the position of the spring after time t. Use the fact that 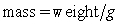 , where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
, where g is the gravitational constant 32 feet per second per second, and that when the spring is first released, its velocity is zero. Round the coefficients to three decimal places.
A) 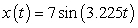
B) 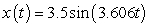
C) 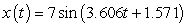
D) 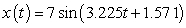
E) 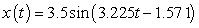
Correct Answer:

Verified
Correct Answer:
Verified
Q12: The willingness of saddle producers to supply
Q13: Newton's Law of Cooling says that the
Q14: When a spring is stretched and then
Q15: Between 1975 and 1980, a country's energy
Q16: The willingness of saddle producers to supply
Q18: The demand for train sets can be
Q19: A person learns a new task at
Q20: Newton's Law of Cooling says that the
Q21: The rate of change in the number
Q22: Find a general solution for the following