Solved

Find the Value of C Which Will Make the Function

Question 31

Multiple Choice

Find the value of c which will make the function Find the value of c which will make the function a pdf on the interval . A) none, since the cosine can be positive or negative B) C) D) a pdf on the interval Find the value of c which will make the function a pdf on the interval . A) none, since the cosine can be positive or negative B) C) D) .


A) none, since the cosine can be positive or negative
B) Find the value of c which will make the function a pdf on the interval . A) none, since the cosine can be positive or negative B) C) D)
C) Find the value of c which will make the function a pdf on the interval . A) none, since the cosine can be positive or negative B) C) D)
D) Find the value of c which will make the function 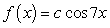a pdf on the interval . A) none, since the cosine can be positive or negative B) 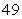C) 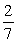D)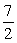

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q26: Find the median of x, rounded to

Q27: Use a comparison to determine whether the

Q28: Use a table of integrals to find

Q29: Find the partial fraction decomposition. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q30: Is the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Is the

Q32: Find the partial fraction decomposition. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q33: Evaluate the integral using integration by parts

Q34: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q35: A given sample of a particular polymer

Q36: Find the indicated limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find