Solved

The Population of Trout in a Certain Overstocked Lake Is

Question 9

Essay

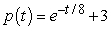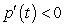The population of trout in a certain overstocked lake is expected to follow the model The population of trout in a certain overstocked lake is expected to follow the model , where p is the population in thousands and t is the time in months. Show that and use this information to determine that the population model never reaches zero. ,
where p is the population in thousands and t is the time in months. Show that The population of trout in a certain overstocked lake is expected to follow the model , where p is the population in thousands and t is the time in months. Show that and use this information to determine that the population model never reaches zero. and use this information to determine that the population model never reaches zero.

Correct Answer:

verifed

Verified

Answer details may vary.
Derivative of p...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q4: Assume that the function has an inverse,

Q5: Use a graph to determine if the

Q6: Show that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Show that

Q7: Evaluate the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q8: Show that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Show that

Q10: A bacterial population starts at 200 and

Q11: A picture hanging in an art gallery

Q12: Determine if the function is one-to-one. If

Q13: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q14: Use logarithmic differentiation to find the derivative