Solved

A Flywheel of Radius R Is Driven by a Reciprocating

Question 27

Multiple Choice

A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . 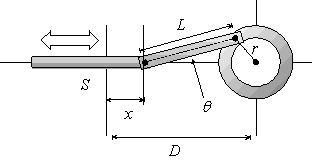A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D) If x represents the displacement of the shaft from its leftmost position, then the angle A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D) between the linking arm and the centerline of the shaft is A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D) . Find the maximum value of A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D) .


A) A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D)
B) A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D)
C) A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is . Find the maximum value of . A) B) C) D)
D) A flywheel of radius r is driven by a reciprocating shaft S and a linking arm L (see figure below) . If x represents the displacement of the shaft from its leftmost position, then the angle between the linking arm and the centerline of the shaft is 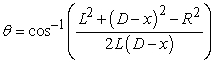. Find the maximum value of 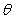. A) 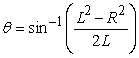B) C) 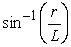D)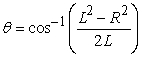

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q22: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q23: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q24: Graph the function. [It may be helpful

Q25: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q26: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q28: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q29: Use the given graph to sketch the

Q30: Sketch the graph of the function. <img

Q31: Show that <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Show that

Q32: Find the derivative of the given function.