Solved

Approximate the Area Under the Curve on the Given Interval

Question 56

Multiple Choice

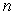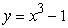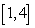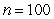
Approximate the area under the curve on the given interval using Approximate the area under the curve on the given interval using rectangles and right-endpoint evaluation. Round to three decimal places. on , A) 58.704 B) 70.381 C) 63.000 D) 61.698 rectangles and right-endpoint evaluation. Round to three decimal places. Approximate the area under the curve on the given interval using rectangles and right-endpoint evaluation. Round to three decimal places. on , A) 58.704 B) 70.381 C) 63.000 D) 61.698 on Approximate the area under the curve on the given interval using rectangles and right-endpoint evaluation. Round to three decimal places. on , A) 58.704 B) 70.381 C) 63.000 D) 61.698 , Approximate the area under the curve on the given interval using rectangles and right-endpoint evaluation. Round to three decimal places. on , A) 58.704 B) 70.381 C) 63.000 D) 61.698


A) 58.704
B) 70.381
C) 63.000
D) 61.698

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q51: Sketch a graph of a function <img

Q52: Suppose that a car can accelerate from

Q53: Suppose that a runner has velocity <img

Q54: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Evaluate the

Q55: Find the general antiderivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q57: Find the derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find the

Q58: Use the graph to determine whether <img

Q59: Determine the position function if the velocity

Q60: Suppose that a car can come to

Q61: Use the graph to estimate the Trapezoidal