Solved

Using the Position Function , Find the Acceleration Function

Question 63

Multiple Choice

Using the position function Using the position function , find the acceleration function. A) B) C) D) , find the acceleration function.


A) Using the position function , find the acceleration function. A) B) C) D)
B) Using the position function , find the acceleration function. A) B) C) D)
C) Using the position function , find the acceleration function. A) B) C) D)
D) Using the position function 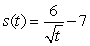, find the acceleration function. A) 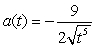B) 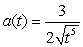C) 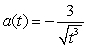D)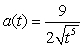

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q58: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q59: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q60: Find an equation of the line tangent

Q61: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q62: Find the derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q64: Find a formula for the nth derivative

Q65: Find all the functions <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q66: Differentiate the function. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Differentiate the

Q67: Determine the real value(s) of x for

Q68: Estimate the slope of the tangent line