Multiple Choice
A second order differential equation can be arranged to the form 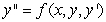 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 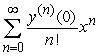 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 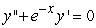 if the initial conditions are
if the initial conditions are 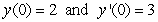 ?
?
A) 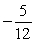
B) 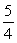
C) 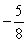
D) 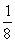
Correct Answer:

Verified
Correct Answer:
Verified
Q20: Find the general solution of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"
Q21: Find the recurrence relation for the general
Q22: A 0.15 kg mass hangs on a
Q23: Determine the form of a particular solution
Q24: Identify the general solution of the the
Q26: Identify the form of a particular solution
Q27: A certain spring is at rest when
Q28: Solve the initial value problem. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"
Q29: A series circuit has a 0.25 henry
Q30: Solve the initial value problem <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"