Solved

A Second Order Differential Equaiton Can Be Arranged to the Form

Question 17

Multiple Choice

A second order differential equaiton can be arranged to the form A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) if the initial conditions are A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D) ?


A) A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D)
B) A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D)
C) A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is , one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation if the initial conditions are ? A) B) C) D)
D) A second order differential equaiton can be arranged to the form , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor series expansion of a function y(x) is 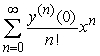, one can differentiate the rearranged second order differential equation to evaluate coefficients of the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0) . What does the fourth-degree Taylor polynomial look like for the solution to the equation 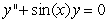if the initial conditions are 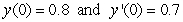? A) 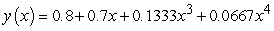B) 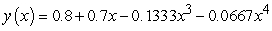C) 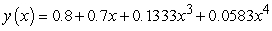D)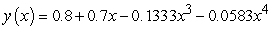

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q12: A series circuit has a 0.1 henry

Q13: Find the general solution of the differential

Q14: Identify the general solution of the the

Q15: Identify the radius of convergence of the

Q16: A pendulum has length 0.22 meter. A

Q18: Consider solutions to the second order differential

Q19: A series circuit has a 0.1 henry

Q20: Find the general solution of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q21: Find the recurrence relation for the general

Q22: A 0.15 kg mass hangs on a