Solved

Compute the Work Done by the Force Field Along

Question 20

Multiple Choice

Compute the work done by the force field Compute the work done by the force field along the curve C, where C is the line segment from (2, 1) to (3, 5) . A) B) C) D) along the curve C, where C is the line segment from (2, 1) to (3, 5) .


A) Compute the work done by the force field along the curve C, where C is the line segment from (2, 1) to (3, 5) . A) B) C) D)
B) Compute the work done by the force field along the curve C, where C is the line segment from (2, 1) to (3, 5) . A) B) C) D)
C) Compute the work done by the force field along the curve C, where C is the line segment from (2, 1) to (3, 5) . A) B) C) D)
D) Compute the work done by the force field along the curve C, where C is the line segment from (2, 1) to (3, 5) . A) 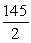B) 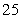C) 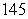D)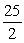

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q15: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Compute using

Q16: Find the outward flux of F over

Q17: Set up a double integral that equals

Q18: Find the gradient field corresponding to <img

Q19: Find the divergence of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q21: Determine whether <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Determine whether

Q22: Set up a double integral that equals

Q23: Use Stokes' Theorem to compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg"

Q24: Find the gradient field corresponding to <img

Q25: Find a potential function and evaluate the