Solved

Which of the Following Is an Arc Length Parameterization of the Given

Question 49

Multiple Choice

Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from to A) B) C) D) to Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from to A) B) C) D)


A) Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from to A) B) C) D)
B) Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from to A) B) C) D)
C) Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from to A) B) C) D)
D) Which of the following is an arc length parameterization of the given two-dimensional curve? The line segment from to A) 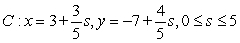B) 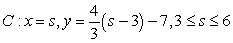C) 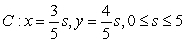D)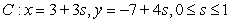

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q44: Use the graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Use

Q45: Match the vector-valued function with its graph.

Q46: Find a parametrically-defined vector <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5869/.jpg" alt="Find

Q47: Sketch the curve and find any points

Q48: Identify and sketch a graph of the

Q50: Use a CAS to estimate the arc

Q51: Find the osculating circle at the given

Q52: Identify and sketch a graph of the

Q53: Match the vector-valued function with its graph.

Q54: Use graphing technology to sketch the curve