Find the Critical Point(s) of the Function

Multiple Choice

Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function.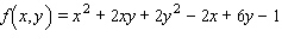

A) (5, - 4) is the critical point, the function has neither a relative maximum nor a relative minimum at this point
B) (5, - 4) is the point of maximum, 18 is the relative maximum
C) (5, - 4) is the point of minimum, - 18 is the relative minimum
D) (5, - 4) is the critical point, it is impossible to determine the relative extrema of the function
E) no critical points