Find the Critical Point(s) of the Function

Multiple Choice

Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function.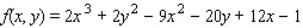

A) (1, 5) and (2, 5) ; saddle point: f(1, 5) = - 46; relative minimum value: f(2, 5) = - 47
B) (2, 5) ; relative maximum value: f(2, 5) = 47
C) (1, 5) ; saddle point: f(1, 5) = - 46
D) (1, 5) and (2, 5) ; relative maximum value: f(1, 5) = - 47; relative minimum value: f(2, 5) = 46
E) there are no critical points