Solved

Determine the Value of the Constant K So That the Function

Question 235

Multiple Choice

Determine the value of the constant k so that the function Determine the value of the constant k so that the function is a probability density function on the interval . A) B) C) D) is a probability density function on the interval Determine the value of the constant k so that the function is a probability density function on the interval . A) B) C) D) .


A) Determine the value of the constant k so that the function is a probability density function on the interval . A) B) C) D)
B) Determine the value of the constant k so that the function is a probability density function on the interval . A) B) C) D)
C) Determine the value of the constant k so that the function is a probability density function on the interval . A) B) C) D)
D) Determine the value of the constant k so that the function 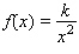is a probability density function on the interval 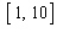. A) 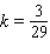B) 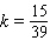C) 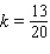D)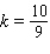

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q230: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Find

Q231: Use the table of integrals to find

Q232: Find the area of the region under

Q233: In a submerged trial run of an

Q234: Determine the value of the constant <img

Q236: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Find

Q237: The number of streets in the downtown

Q238: Find the indefinite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Find

Q239: The amount of nitrogen dioxide, a brown

Q240: Evaluate the following improper integral whenever it