Solved

Determine Whether the Statement Is True or False

Question 82

Multiple Choice

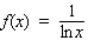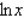Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. 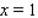is continuous on Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. .


A) The function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. is continuous but zero when
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. , then the function
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. is not continuous in
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. , so the statement is false.
B) The function Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. is continuous and nonzero on
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. , then the function
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function is continuous and nonzero on , then the function is continuous in , so the statement is true. is continuous in
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. The function is continuous on . A) The function is continuous but zero when , then the function is not continuous in , so the statement is false. B) The function 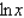is continuous and nonzero on 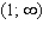, then the function 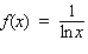is continuous in , so the statement is true. , so the statement is true.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q77: Use logarithms to solve the equation for

Q78: Eleni, who is now 55 years old,

Q79: Use the laws of logarithms to simplify

Q80: Use the laws of logarithms to simplify

Q81: Find the second derivative of the function.

Q83: Find the derivative of the function. <img

Q84: Find the second derivative of the function.

Q85: The price of a certain commodity in

Q86: The radioactive element polonium decays according to

Q87: Find the derivative of the function. <img