Solved

Show That the Function Has No Relative Extrema on

Question 11

Multiple Choice

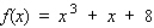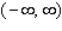Show that the function Show that the function has no relative extrema on . A) The function has no relative extrema by definition of the derivation. B) The derivation of the function is . At every point the derivative exists and does not equal to 0. So by definition the function has no relative extrema on this interval. C) The function has no relative extrema because does not equal to 0 at any point. 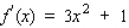has no relative extrema on Show that the function has no relative extrema on . A) The function has no relative extrema by definition of the derivation. B) The derivation of the function is . At every point the derivative exists and does not equal to 0. So by definition the function has no relative extrema on this interval. C) The function has no relative extrema because does not equal to 0 at any point. .


A) The function has no relative extrema by definition of the derivation.
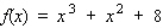B) The derivation of the function Show that the function has no relative extrema on . A) The function has no relative extrema by definition of the derivation. B) The derivation of the function is . At every point the derivative exists and does not equal to 0. So by definition the function has no relative extrema on this interval. C) The function has no relative extrema because does not equal to 0 at any point. is
Show that the function has no relative extrema on . A) The function has no relative extrema by definition of the derivation. B) The derivation of the function is . At every point the derivative exists and does not equal to 0. So by definition the function has no relative extrema on this interval. C) The function has no relative extrema because does not equal to 0 at any point. . At every point the derivative exists and does not equal to 0. So by definition the function has no relative extrema on this interval.
C) The function has no relative extrema because Show that the function has no relative extrema on . A) The function has no relative extrema by definition of the derivation. B) The derivation of the function is . At every point the derivative exists and does not equal to 0. So by definition the function has no relative extrema on this interval. C) The function has no relative extrema because does not equal to 0 at any point. does not equal to 0 at any point.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q6: The average speed of a vehicle on

Q7: The concentration (in milligrams/cubic centimeter) of a

Q8: Find the relative maxima and relative minima,

Q9: Find the absolute maximum value and the

Q10: Find the inflection points of the following

Q12: Find the relative maxima and relative minima,

Q13: Find the relative maxima and relative minima,

Q14: Find the absolute maximum value and the

Q15: The height (in feet) attained by a

Q16: Find the inflection points, if any, of