Solved

Let F Be the Function Defined by

Question 138

Essay

Let f be the function defined by Let f be the function defined by . Find the differential of f. __________ Find the approximate change in y if x changes from 3 to 3.07. __________ Find the actual change in y if x changes from 3 to 3.07. __________ .
Find the differential of f. Let f be the function defined by . Find the differential of f. __________ Find the approximate change in y if x changes from 3 to 3.07. __________ Find the actual change in y if x changes from 3 to 3.07. __________ __________
Find the approximate change in y if x changes from 3 to 3.07. Let f be the function defined by . Find the differential of f. __________ Find the approximate change in y if x changes from 3 to 3.07. __________ Find the actual change in y if x changes from 3 to 3.07. __________ __________
Find the actual change in y if x changes from 3 to 3.07. Let f be the function defined by 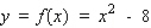. Find the differential of f. 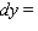__________ Find the approximate change in y if x changes from 3 to 3.07. __________ Find the actual change in y if x changes from 3 to 3.07. __________ __________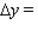

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q133: Find the derivative of the function. <img

Q134: The total weekly cost (in dollars) incurred

Q135: Find the third derivative of the function.

Q136: The population of Americans age 55 yr

Q137: Find the second derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Find

Q139: The number of persons aged 18-64 receiving

Q140: Find the derivative of the function. <img

Q141: According to the South Coast Air Quality

Q142: Find the slope and an equation of

Q143: Find the differential of the function. <img