Solved

The Demand Equation Is

Question 171

Multiple Choice

The demand equation is The demand equation is . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at . A) B) C) D) . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at The demand equation is . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at . A) B) C) D) .


A) The demand equation is . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at . A) B) C) D)
B) The demand equation is . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at . A) B) C) D)
C) The demand equation is . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at . A) B) C) D)
D) The demand equation is . Compute the elasticity of demand and determine whether the demand is elastic, unitary, or inelastic at 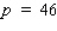. A) 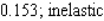B) 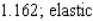C) 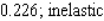D)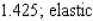

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q166: Find the derivative of the function. <img

Q167: Find the derivative of the function by

Q168: Find the derivative of the function and

Q169: Find the differential of the function. <img

Q170: Find the first and second derivatives of

Q172: Use a differential to approximate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg"

Q173: Find the limit by evaluating the derivative

Q174: Suppose f and g are functions that

Q175: Suppose <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6026/.jpg" alt="Suppose .

Q176: Find the first and second derivatives of