Intelligence Quotient (IQ) Scores Are Assumed to Be Normally Distributed $\int _ { 0 } ^ { 2 } p ( x ) d x$

Essay

Intelligence Quotient (IQ) scores are assumed to be normally distributed in the population. The probability that a person selected at random from the general population will have an IQ between 100 and 120 is given by $\int _ { 0 } ^ { 2 } p ( x ) d x$ Use the graph of p (x) graphed below to answer the questions which follow: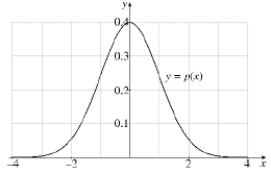
(a) Use Simpson's Rule with n = 4 to approximate $\int _ { 0 } ^ { 2 } p ( x ) d x$
(b) The probability that a person selected from the general population will have an IQ score between 80 and 120 is given by $\int _ { - 2 } ^ { 2 } p ( x ) d x$ What is the approximate value of $\int _ { - 2 } ^ { 2 } p ( x ) d x ?$ (c) Since p (x) represents a probability distribution, the entire area of the region under the graph is exactly 1. Using this information, what is the approximate probability that a person selected at random from the general population will have an IQ score over 120?