Essay
The region D in shown below is bounded by x = 1, , and . 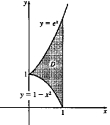 (a) Compute by finding .(b) Write down the integral or integrals needed to compute with the order of integration reversed.
(a) Compute by finding .(b) Write down the integral or integrals needed to compute with the order of integration reversed.
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q74: Use the change of variables u
Q75: Evaluate <span class="ql-formula" data-value="\int _
Q76: Evaluate the iterated integral <span
Q77: Find the centroid of <span
Q78: Evaluate the double integral <span
Q80: Calculate the iterated integral <span
Q81: Let <span class="ql-formula" data-value="f (
Q82: Find the Jacobian of the transformation
Q83: Find the volume of the region
Q84: Evaluate the double integral <span