Solved

Find the Taylor Series About C = 5 and Its

Question 65

Multiple Choice

Find the Taylor series about c = 5 and its interval of convergence. Find the Taylor series about c = 5 and its interval of convergence. A) B) C) D)


A) Find the Taylor series about c = 5 and its interval of convergence. A) B) C) D)
B) Find the Taylor series about c = 5 and its interval of convergence. A) B) C) D)
C) Find the Taylor series about c = 5 and its interval of convergence. A) B) C) D)
D) Find the Taylor series about c = 5 and its interval of convergence. 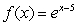A) 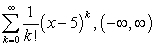B) 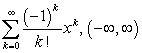C) D)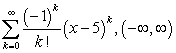

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q60: Determine whether the sequence converges or diverges.

Q61: Estimate the sum of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Estimate

Q62: Determine all values of p for which

Q63: Estimate the error in using <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"

Q64: Determine whether the sequence converges or diverges.

Q66: Determine whether the series is convergent or

Q67: Determine whether <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Determine whether

Q68: Determine if <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Determine if

Q69: Find the MacLaurin series and its interval

Q70: Determine all values of p for which