Solved

Determine the Position Function If the Velocity Function Is

Question 139

Multiple Choice

Determine the position function if the velocity function is Determine the position function if the velocity function is and the initial position is . A) B) C) D) and the initial position is Determine the position function if the velocity function is and the initial position is . A) B) C) D) .


A) Determine the position function if the velocity function is and the initial position is . A) B) C) D)
B) Determine the position function if the velocity function is and the initial position is . A) B) C) D)
C) Determine the position function if the velocity function is and the initial position is . A) B) C) D)
D) Determine the position function if the velocity function is 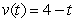and the initial position is 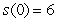. A) 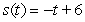B) 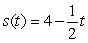C) 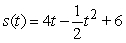D)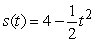

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q134: Use the given information about <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"

Q135: Evaluate the definite integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Evaluate

Q136: Use summation rules to compute the sum.

Q137: Evaluate the integral exactly. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Evaluate

Q138: Estimate the integral numerically. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Estimate

Q140: Compute the sum and the limit of

Q141: Write the given (signed) area as an

Q142: Find a value of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find

Q143: Compute the sum of the form <img

Q144: Evaluate the integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Evaluate the