Solved

Determine the Position Function If the Acceleration Function Is

Question 40

Multiple Choice

Determine the position function if the acceleration function is Determine the position function if the acceleration function is , the initial velocity is , and the initial position is . A) B) C) D) , the initial velocity is Determine the position function if the acceleration function is , the initial velocity is , and the initial position is . A) B) C) D) , and the initial position is Determine the position function if the acceleration function is , the initial velocity is , and the initial position is . A) B) C) D) .


A) Determine the position function if the acceleration function is , the initial velocity is , and the initial position is . A) B) C) D)
B) Determine the position function if the acceleration function is , the initial velocity is , and the initial position is . A) B) C) D)
C) Determine the position function if the acceleration function is , the initial velocity is , and the initial position is . A) B) C) D)
D) Determine the position function if the acceleration function is 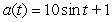, the initial velocity is 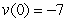, and the initial position is . A) B) 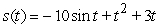C) 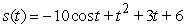D)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q35: Use Riemann sums and a limit to

Q36: Compute the error (the difference between the

Q37: Use the given substitution to evaluate the

Q38: Find the average value of the function

Q39: For a business using just-in-time inventory, a

Q41: Find an antiderivative by reversing the chain

Q42: Evaluate the integral by computing the limit

Q43: Translate into summation notation. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Translate

Q44: Find the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find the

Q45: Use Simpson's Rule with <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Use