Solved

Let and Define

Question 29

Essay

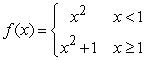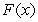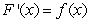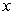Let Let and define . Show that is continuous but that it is not true that for all . Explain why this does not contradict the Fundamental Theorem of Calculus. and define Let and define . Show that is continuous but that it is not true that for all . Explain why this does not contradict the Fundamental Theorem of Calculus. . Show that Let and define . Show that is continuous but that it is not true that for all . Explain why this does not contradict the Fundamental Theorem of Calculus. is continuous but that it is not true that Let and define . Show that is continuous but that it is not true that for all . Explain why this does not contradict the Fundamental Theorem of Calculus. for all Let and define . Show that is continuous but that it is not true that for all . Explain why this does not contradict the Fundamental Theorem of Calculus. . Explain why this does not contradict the Fundamental Theorem of Calculus.

Correct Answer:

verifed

Verified

For blured image : blured image For blured image : blured image Thus, blured image is defined piecew...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q24: Approximate the area under the curve on

Q25: Compute the Trapezoidal Rule approximation by hand

Q26: Find the general antiderivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find

Q27: Translate the following calculation into summation notation

Q28: Compute <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Compute ,

Q30: Sketch a graph of a function <img

Q31: Find the derivative <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find the

Q32: Find all functions satisfying the given conditions.

Q33: Evaluate the derivative using properties of logarithms

Q34: Find the general antiderivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Find