Solved

Using Newton's Method, Approximate the Root of the Following Equation

Question 25

Multiple Choice

Using Newton's method, approximate the root of the following equation to at least six-digit accuracy. Using Newton's method, approximate the root of the following equation to at least six-digit accuracy. 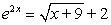A) 0.817880 B) 0.839580 C) 0.807714 D) 0.827880


A) 0.817880
B) 0.839580
C) 0.807714
D) 0.827880

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: Find the elasticity of demand if <img

Q21: Use linear approximation of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Use

Q22: Graph the function and completely discuss the

Q23: Sketch the graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg" alt="Sketch

Q24: Using the critical numbers of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"

Q26: Suppose that at the price <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"

Q27: Determine the following significant features by hand

Q28: Determine, by hand, the interval(s) where <img

Q29: A plane is located at <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"

Q30: The mass of the first x meters