Solved

Use Lagrange Multipliers to Find the Closest Point on the Given

Question 78

Multiple Choice

Use Lagrange multipliers to find the closest point on the given curve to the indicated point. Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)


A) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)
B) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)
C) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) C) D)
D) Use Lagrange multipliers to find the closest point on the given curve to the indicated point. A) B) 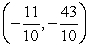C) 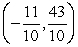D)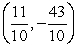

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q73: Find a function with the given properties.

Q74: Show that the indicated limit exists. <img

Q75: Calculate the first two steps of the

Q76: Locate all critical points and classify them.

Q77: Numerically approximate all critical points. Classify each.

Q79: Suppose the production of a firm is

Q80: Use a graphing utility to sketch the

Q81: Use the given contour plot to estimate

Q82: Find the indicated partial derivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2342/.jpg"

Q83: Use the contour plot to estimate <img