Multiple Choice
A company is developing its weekly production plan. The company produces two products, A and B, which are processed in two departments. Setting up each batch of A requires $60 of labor while setting up a batch of B costs $80. Each unit of A generates a profit of $17 while a unit of B earns a profit of $21. The company can sell all the units it produces. The data for the problem are summarized below. 
What is the appropriate formula to use in cell E8 of the following Excel implementation of the ILP model for this problem?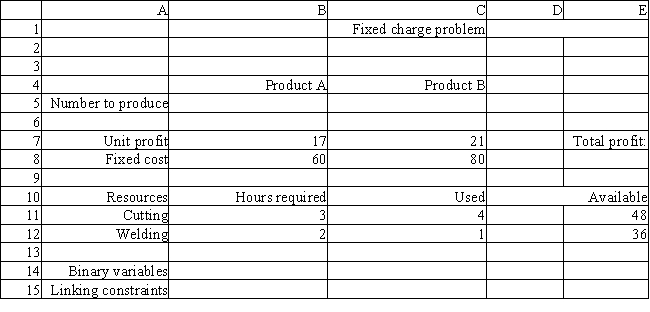 
A) =SUMPRODUCT(B5:C5,B7:C7) − SUMPRODUCT(B8:C8,B14:C14)
B) =SUMPRODUCT(B8:C8,B14:C14) − SUMPRODUCT(B5:C5,B7:C7)
C) =SUMPRODUCT(B5:C5,B7:C7) − B8:C8
D) =SUMPRODUCT(B5:C5,B7:C7) − SUMPRODUCT(B8:C8,B15:C15)
Correct Answer:
Verified
Correct Answer:
Verified
Q44: The concept of an upper bound in
Q45: An ILP problem has 5 binary decision
Q46: Pure IP formulation requires that:<br>A) all decision
Q47: What does the Analytic Solver Platform integer
Q48: A company is developing its weekly production
Q50: Suppose you want to minimize an objective
Q51: A company is developing its weekly production
Q52: In the B & B algorithm, B
Q53: A manufacturing company has costs associated with
Q54: The objective function value for the ILP