Multiple Choice
The introductory biology class at State University is conducting a study of water quality in their local community.The population mean of a certain beneficial bacteria found in drinking water ( 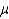 ) is 100,with
) is 100,with 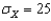 .The bacteria counts from the community are given below.Use a two-tailed rejection region with a total area of 0.05.What should you conclude?
.The bacteria counts from the community are given below.Use a two-tailed rejection region with a total area of 0.05.What should you conclude? 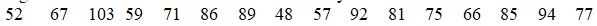
A) Since the z-value falls within the region of rejection,we should conclude this sample mean likely represents some other population.
B) Since the z-value does not fall within the region of rejection,we should not conclude this sample mean represents some other population.
C) Since the z-value falls within the region of rejection,we should not conclude this sample mean represents some other population.
D) Since the z-value does not fall within the region of rejection,we should conclude this sample mean likely represents some other population.
Correct Answer:

Verified
Correct Answer:
Verified
Q16: The probability of getting heads on a
Q17: If we decide to reject the idea
Q18: How can we determine the representativeness of
Q19: When we select a sample so that
Q20: The scores that lie in the tails
Q22: There are 26 red cards in a
Q23: If we decide not to reject the
Q24: Which of the following is not true
Q25: A cognitive psychologist tested whether people spend
Q26: Which of the following is the criterion