Solved

A Plane Lamina with Constant Density Occupies a Region

Question 12

Multiple Choice

A plane lamina with constant density A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E) occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E) Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E) .


A) A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E)
B) A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E)
C) A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E)
D) A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and . A) B) C) D) E)
E) A plane lamina with constant density 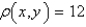occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are 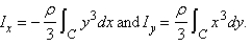Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0) ,(4,0) , (4,5) and 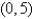. A) 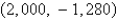B) 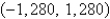C) 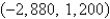D) 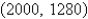E)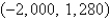

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q7: Evaluate the surface integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Evaluate

Q8: Determine whether or not F is a

Q9: Evaluate the surface integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Evaluate

Q10: Suppose that F is an inverse square

Q11: Match the equation with one of the

Q13: Use Stoke's theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg"

Q14: Find the curl of the vector field

Q15: The temperature at the point <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg"

Q16: Use Stokes' Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg"

Q17: Use Stokes' Theorem to evaluate <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg"