Solved

Let Where

Question 5

Multiple Choice

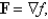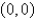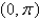Let Let where . Which of the following equations does the line segment from to satisfy? A) B) C) none of these where Let where . Which of the following equations does the line segment from to satisfy? A) B) C) none of these . Which of the following equations does the line segment from Let where . Which of the following equations does the line segment from to satisfy? A) B) C) none of these to Let where . Which of the following equations does the line segment from to satisfy? A) B) C) none of these satisfy?


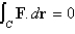
A) Let where . Which of the following equations does the line segment from to satisfy? A) B) C) none of these
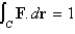
B) Let where . Which of the following equations does the line segment from to satisfy? A) B) C) none of these
C) none of these

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Use Green's Theorem to find the work

Q2: Find the moment of inertia about the

Q3: Find a function f such that <img

Q4: Determine whether or not vector field is

Q6: A thin wire is bent into the

Q7: Evaluate the surface integral <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Evaluate

Q8: Determine whether or not F is a

Q9: Evaluate the surface integral. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Evaluate

Q10: Suppose that F is an inverse square

Q11: Match the equation with one of the