Solved

Suppose (1,1)is a Critical Point of a Function F with Continuous

Question 17

Multiple Choice

Suppose (1,1) is a critical point of a function f with continuous second derivatives. In the case of , , 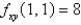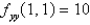what can you say about f ?

A) f has a local maximum at (1,1)
B) f has a saddle point at (1,1)
C) f has a local minimum at (1,1)

Related Questions

Q12: Find the absolute minimum value of the

Q13: Find the points on the surface <img

Q14: Determine the largest set on which the

Q15: Find the critical points of the function.

Q16: Suppose that over a certain region of

Q18: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Find .

Q19: Find the local maximum,and minimum value and

Q20: Determine where the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Determine

Q21: Find the equation of the tangent plane

Q22: Use Lagrange multipliers to find the maximum