Solved

Approximate by a Taylor Polynomial with Degree N at the Number

Question 13

Multiple Choice

Approximate by a Taylor polynomial with degree n at the number a. Approximate by a Taylor polynomial with degree n at the number a. A) B) C) D) E)


A) Approximate by a Taylor polynomial with degree n at the number a. A) B) C) D) E)
B) Approximate by a Taylor polynomial with degree n at the number a. A) B) C) D) E)
C) Approximate by a Taylor polynomial with degree n at the number a. A) B) C) D) E)
D) Approximate by a Taylor polynomial with degree n at the number a. A) B) C) D) E)
E) Approximate by a Taylor polynomial with degree n at the number a. 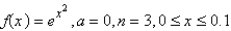A) B) 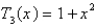C) 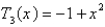D) 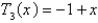E)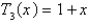

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q8: Find the radius of convergence and the

Q9: Approximate by a Taylor polynomial with degree

Q10: Find a power series representation for the

Q11: Determine whether the sequence is increasing,decreasing,or not

Q12: Evaluate the indefinite integral as an infinite

Q14: Determine whether the series is absolutely convergent,conditionally

Q15: Determine whether the geometric series converges or

Q16: Which of the given series are absolutely

Q17: A right triangle ABC is given with

Q18: Determine whether the given series converges or