Multiple Choice
Assume that is a one-to-one function.
(a) If 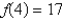 ,what is
,what is 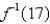 ?
?
(b) If  ,what is
,what is 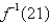 ?
?
A) 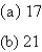
B) 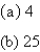
C) 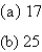
D) 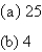
E) 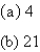
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q14: Find an equation of the tangent line
Q15: The area of the region that lies
Q16: A telephone line hangs between two poles
Q17: Use logarithmic differentiation to find the derivative
Q18: Find the limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Find the
Q20: Find the exact value of the expression
Q21: Use the laws of logarithms to expand
Q22: Evaluate the limit using l'Hôpital's Rule. <img
Q23: The velocity function (in meters per second)is
Q24: Find the derivative. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2067/.jpg" alt="Find the