Solved

The Function Satisfies the Hypotheses of Rolle's Theorem on the Interval

Question 7

Multiple Choice

The function The function satisfies the hypotheses of Rolle's Theorem on the interval .Find all values of c that satisfy the conclusion of the theorem. A) B) C) D) satisfies the hypotheses of Rolle's Theorem on the interval The function satisfies the hypotheses of Rolle's Theorem on the interval .Find all values of c that satisfy the conclusion of the theorem. A) B) C) D) .Find all values of c that satisfy the conclusion of the theorem.


A) The function satisfies the hypotheses of Rolle's Theorem on the interval .Find all values of c that satisfy the conclusion of the theorem. A) B) C) D)
B) The function satisfies the hypotheses of Rolle's Theorem on the interval .Find all values of c that satisfy the conclusion of the theorem. A) B) C) D)
C) The function satisfies the hypotheses of Rolle's Theorem on the interval .Find all values of c that satisfy the conclusion of the theorem. A) B) C) D)
D) The function satisfies the hypotheses of Rolle's Theorem on the interval .Find all values of c that satisfy the conclusion of the theorem. A) 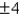B) C) 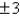D)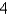

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q2: Find the critical number(s),if any,of the function

Q3: Find the number c that satisfies the

Q4: Find the most general antiderivative of the

Q5: Find the absolute maximum and absolute minimum

Q6: The graph of the first derivative <img

Q8: Use Newton's method with the specified initial

Q9: Determine where the graph of the function

Q10: Find all the critical numbers of the

Q11: The sum of two positive numbers is

Q12: Find the position function of a particle