Solved

If j, an Unbiased Estimator of 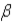j, Is

Question 4

Multiple Choice

If If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j, an unbiased estimator of If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j, is also a consistent estimator of 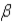If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j, then when the sample size tends to infinity:


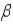A) the distribution of If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j collapses to a single value of zero.
B) the distribution of If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j diverges away from a single value of zero.
C) the distribution of
If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j collapses to the single point
If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j.
D) the distribution of
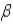If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j diverges away from
If <sub>j</sub>, an unbiased estimator of <sub>j</sub>, is also a consistent estimator of <sub>j</sub>, then when the sample size tends to infinity: A) the distribution of <sub>j</sub> collapses to a single value of zero. B) the distribution of <sub>j</sub> diverges away from a single value of zero. C) the distribution of <sub>j</sub> collapses to the single point <sub>j</sub>. D) the distribution of <sub>j</sub> diverges away from <sub>j</sub>. j.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: Which of the following statements is true?<br>A)The

Q2: The Cauchy-Schwartz inequality implies that the asymptotic

Q5: A useful rule of thumb is that

Q7: The n-R-squared statistic also refers to the:<br>A)F

Q10: In the multiple regression model <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2133/.jpg"

Q11: The LM statistic follows a:<br>A)t distribution.<br>B)f distribution.<br>C)<br><img

Q12: If Cov(z,x) ≠ 0, then z and

Q14: Even if the error terms in a

Q22: The LM statistic requires estimation of the

Q25: Which of the following statements is true