Multiple Choice
A covariance stationary time series is weakly dependent if:
A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 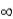 as h
as h  0.
0.
B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h 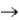
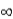 .
.
C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h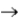
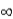 .
.
D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to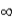 as h
as h
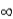 .
.
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Which of the following is assumed in
Q4: Unit root processes, such as a random
Q8: In the model y<sub>t</sub> = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2133/.jpg"
Q8: Which of the following statements is true?<br>A)A
Q10: The model y<sub>t</sub> = e<sub>t</sub> + <img
Q10: If a process is said to be
Q12: A process is stationary if:<br>A)any collection of
Q13: The model x<sub>t</sub> = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2133/.jpg" alt="The
Q20: Which of the following statements is true?<br>A)A
Q27: Which of the following statements is true