Multiple Choice
Let 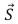 = (1 m)
= (1 m) 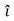 + (2 m)
+ (2 m) 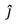 + (2 m)
+ (2 m) 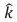 and
and 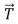 = (3 m)
= (3 m) 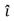 + (4 m)
+ (4 m) 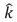 .The angle between these two vectors is given by:
.The angle between these two vectors is given by:
A) cos-1(14/15)
B) cos-1(11/225)
C) cos-1(104/225)
D) cos-1(11/15)
E) cannot be found since 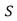 and
and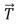 do not lie in the same plane
do not lie in the same plane
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Two vectors lie with their tails at
Q3: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt=" Let
Q4: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt="If =
Q5: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt="Let =
Q6: Vectors <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt="Vectors and
Q8: If <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt="If =
Q9: The value of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt="The value
Q10: The two vectors (3 m) <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg"
Q11: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6585/.jpg" alt="Let =
Q12: Two vectors have magnitudes of 10